ZFC and propositional logic

Using a mélange of mathematical syntaxes, we mechanize some exercises from Tao's excellent book

Overture

Let us informally define sets and set membership . A set is an unordered collection of objects, with the set itself being an object. Set membership checks whether a given object is contained within a set:

The axiom of substitution uses the definition of equality:

The axiom of substitution is preserved for all sets only defined in terms of and .

Verify that set equality is reflexive, symmetric, and transitive.

Goal:

Hypothesis:

Proof.

Qed.

Prove that the following sets are distinct: .

Hypothesis:

Lemma:

Proof.

Qed.

Show that, for any set ,

Hypothesis:

Proof.

Qed.

Show that, for any three sets , , and .

Hypothesis:

Proof.

Qed.

Show that, for any two sets ,

Hypothesis:

Proof.

Qed.

(3.3.4) Show that injective corresponds to left-cancelable, and dually, surjective corresponds to right-cancelable, in function composition.

For this proof, we use natural deductions, as introduced in Dowek's Proofs in Theories Ch. 1.

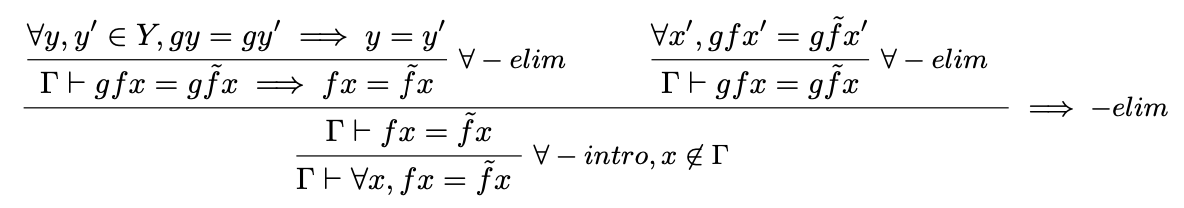
where